The valence electrons in the atom were described by Richard Abegg in 1904. Stoner incorporated Sommerfeld's third quantum number into the description of electron shells, and correctly predicted the shell structure of sulfur to be 2.8.6. Neon has eight valence electrons in its outer shell. This means it does not easily react with other elements, as it has a full octet. Which other element behaves similarly? Carbon lead iodine helium. For example, in above, Helium (He) and Neon (Ne) have outer valence shells that are completely filled, so neither has a tendency to gain or lose electrons. Therefore, Helium and Neon, two of the so-called Noble gases, exist in free atomic form and do not usually form chemical bonds with other atoms. The total number of electrons present in the valence shell of an atom is called valence electrons, and there is only one electron present in the valence shell of neon (2s²2p⁶). Thus, neon has eight valence electrons. Valency of Neon (Ne). In the periodic table, each column is called a group. The elements in each group have the same number of electrons in the outer orbital. Those outer electrons are also called valence electrons. See the attached figure. Silicon and Carbon have the same number of valence.
How Many Neon Valence Electrons
Learning Objectives
- To understand the basics of adding electrons to atomic orbitals
- To understand the basics of the Aufbau principle
The electron configuration of an element is the arrangement of its electrons in its atomic orbitals. By knowing the electron configuration of an element, we can predict and explain a great deal of its chemistry.
The Aufbau Principle
We construct the periodic table by following the aufbau principle (from German, meaning “building up”). First we determine the number of electrons in the atom; then we add electrons one at a time to the lowest-energy orbital available without violating the Pauli principle. We use the orbital energy diagram of Figure (PageIndex{1}), recognizing that each orbital can hold two electrons, one with spin up ↑, corresponding to ms = +½, which is arbitrarily written first, and one with spin down ↓, corresponding to ms = −½. A filled orbital is indicated by ↑↓, in which the electron spins are said to be paired. Here is a schematic orbital diagram for a hydrogen atom in its ground state:
From the orbital diagram, we can write the electron configuration in an abbreviated form in which the occupied orbitals are identified by their principal quantum number n and their value of l (s, p, d, or f), with the number of electrons in the subshell indicated by a superscript. For hydrogen, therefore, the single electron is placed in the 1s orbital, which is the orbital lowest in energy (Figure (PageIndex{1})), and the electron configuration is written as 1s1 and read as “one-s-one.”
A neutral helium atom, with an atomic number of 2 (Z = 2), has two electrons. We place one electron in the orbital that is lowest in energy, the 1s orbital. From the Pauli exclusion principle, we know that an orbital can contain two electrons with opposite spin, so we place the second electron in the same orbital as the first but pointing down, so that the electrons are paired. The orbital diagram for the helium atom is therefore
written as 1s2, where the superscript 2 implies the pairing of spins. Otherwise, our configuration would violate the Pauli principle.
The next element is lithium, with Z = 3 and three electrons in the neutral atom. We know that the 1s orbital can hold two of the electrons with their spins paired. Figure 6.29 tells us that the next lowest energy orbital is 2s, so the orbital diagram for lithium is
This electron configuration is written as 1s22s1.
The next element is beryllium, with Z = 4 and four electrons. We fill both the 1s and 2s orbitals to achieve a 1s22s2 electron configuration:
When we reach boron, with Z = 5 and five electrons, we must place the fifth electron in one of the 2p orbitals. Because all three 2p orbitals are degenerate, it doesn’t matter which one we select. The electron configuration of boron is 1s22s22p1:
At carbon, with Z = 6 and six electrons, we are faced with a choice. Should the sixth electron be placed in the same 2p orbital that already has an electron, or should it go in one of the empty 2p orbitals? If it goes in an empty 2p orbital, will the sixth electron have its spin aligned with or be opposite to the spin of the fifth? In short, which of the following three orbital diagrams is correct for carbon, remembering that the 2p orbitals are degenerate?
Because of electron-electron interactions, it is more favorable energetically for an electron to be in an unoccupied orbital than in one that is already occupied; hence we can eliminate choice a. Similarly, experiments have shown that choice b is slightly higher in energy (less stable) than choice c because electrons in degenerate orbitals prefer to line up with their spins parallel; thus, we can eliminate choice b. Choice c illustrates Hund’s rule (named after the German physicist Friedrich H. Hund, 1896–1997), which today says that the lowest-energy electron configuration for an atom is the one that has the maximum number of electrons with parallel spins in degenerate orbitals. By Hund’s rule, the electron configuration of carbon, which is 1s22s22p2, is understood to correspond to the orbital diagram shown in c. Experimentally, it is found that the ground state of a neutral carbon atom does indeed contain two unpaired electrons.
Neon Valence Electrons And Energy Levels
When we get to nitrogen (Z = 7, with seven electrons), Hund’s rule tells us that the lowest-energy arrangement is
with three unpaired electrons. The electron configuration of nitrogen is thus 1s22s22p3.
At oxygen, with Z = 8 and eight electrons, we have no choice. One electron must be paired with another in one of the 2p orbitals, which gives us two unpaired electrons and a 1s22s22p4 electron configuration. Because all the 2p orbitals are degenerate, it doesn’t matter which one has the pair of electrons.
Similarly, fluorine has the electron configuration 1s22s22p5:
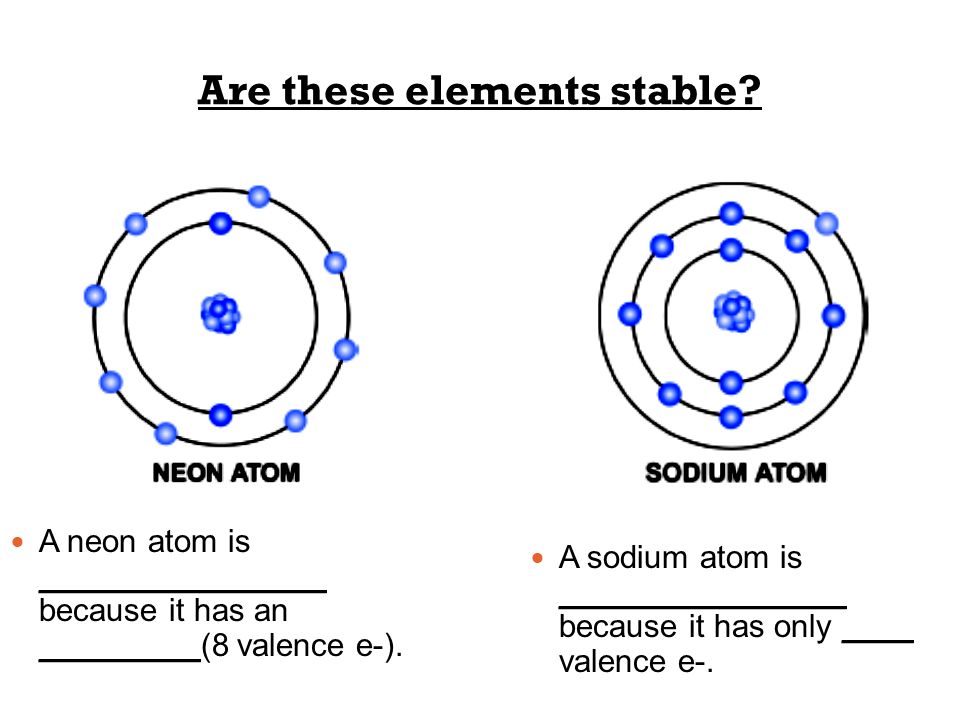
When we reach neon, with Z = 10, we have filled the 2p subshell, giving a 1s22s22p6 electron configuration:
Notice that for neon, as for helium, all the orbitals through the 2p level are completely filled. This fact is very important in dictating both the chemical reactivity and the bonding of helium and neon, as you will see.
Valence Electrons
As we continue through the periodic table in this way, writing the electron configurations of larger and larger atoms, it becomes tedious to keep copying the configurations of the filled inner subshells. In practice, chemists simplify the notation by using a bracketed noble gas symbol to represent the configuration of the noble gas from the preceding row because all the orbitals in a noble gas are filled. For example, [Ne] represents the 1s22s22p6 electron configuration of neon (Z = 10), so the electron configuration of sodium, with Z = 11, which is 1s22s22p63s1, is written as [Ne]3s1:
| Neon | Z = 10 | 1s22s22p6 |
| Sodium | Z = 11 | 1s22s22p63s1 = [Ne]3s1 |
Because electrons in filled inner orbitals are closer to the nucleus and more tightly bound to it, they are rarely involved in chemical reactions. This means that the chemistry of an atom depends mostly on the electrons in its outermost shell, which are called the valence electrons. The simplified notation allows us to see the valence-electron configuration more easily. Using this notation to compare the electron configurations of sodium and lithium, we have:
| Sodium | 1s22s22p63s1 = [Ne]3s1 |
| Lithium | 1s22s1 = [He]2s1 |
It is readily apparent that both sodium and lithium have one s electron in their valence shell. We would therefore predict that sodium and lithium have very similar chemistry, which is indeed the case.
As we continue to build the eight elements of period 3, the 3s and 3p orbitals are filled, one electron at a time. This row concludes with the noble gas argon, which has the electron configuration [Ne]3s23p6, corresponding to a filled valence shell.
Example (PageIndex{1}): Electronic Configuration of Phoshorus
Draw an orbital diagram and use it to derive the electron configuration of phosphorus, Z = 15. What is its valence electron configuration?
Given: atomic number
Asked for: orbital diagram and valence electron configuration for phosphorus
Strategy:
- Locate the nearest noble gas preceding phosphorus in the periodic table. Then subtract its number of electrons from those in phosphorus to obtain the number of valence electrons in phosphorus.
- Referring to Figure Figure (PageIndex{1}), draw an orbital diagram to represent those valence orbitals. Following Hund’s rule, place the valence electrons in the available orbitals, beginning with the orbital that is lowest in energy. Write the electron configuration from your orbital diagram.
- Ignore the inner orbitals (those that correspond to the electron configuration of the nearest noble gas) and write the valence electron configuration for phosphorus.
Solution:
A Because phosphorus is in the third row of the periodic table, we know that it has a [Ne] closed shell with 10 electrons. We begin by subtracting 10 electrons from the 15 in phosphorus.
B The additional five electrons are placed in the next available orbitals, which Figure (PageIndex{1}) tells us are the 3s and 3p orbitals:
Because the 3s orbital is lower in energy than the 3p orbitals, we fill it first:
Hund’s rule tells us that the remaining three electrons will occupy the degenerate 3p orbitals separately but with their spins aligned:
The electron configuration is [Ne]3s23p3.
C We obtain the valence electron configuration by ignoring the inner orbitals, which for phosphorus means that we ignore the [Ne] closed shell. This gives a valence-electron configuration of 3s23p3.
Exercise (PageIndex{1})
Draw an orbital diagram and use it to derive the electron configuration of chlorine, Z = 17. What is its valence electron configuration?
Answer:
[Ne]3s23p5; 3s23p5
The general order in which orbitals are filled is depicted in Figure (PageIndex{2}). Subshells corresponding to each value of n are written from left to right on successive horizontal lines, where each row represents a row in the periodic table. The order in which the orbitals are filled is indicated by the diagonal lines running from the upper right to the lower left. Accordingly, the 4s orbital is filled prior to the 3d orbital because of shielding and penetration effects. Consequently, the electron configuration of potassium, which begins the fourth period, is [Ar]4s1, and the configuration of calcium is [Ar]4s2. Five 3d orbitals are filled by the next 10 elements, the transition metals, followed by three 4p orbitals. Notice that the last member of this row is the noble gas krypton (Z = 36), [Ar]4s23d104p6 = [Kr], which has filled 4s, 3d, and 4p orbitals. The fifth row of the periodic table is essentially the same as the fourth, except that the 5s, 4d, and 5p orbitals are filled sequentially.
The sixth row of the periodic table will be different from the preceding two because the 4f orbitals, which can hold 14 electrons, are filled between the 6s and the 5d orbitals. The elements that contain 4f orbitals in their valence shell are the lanthanides. When the 6p orbitals are finally filled, we have reached the next (and last known) noble gas, radon (Z = 86), [Xe]6s24f145d106p6 = [Rn]. In the last row, the 5f orbitals are filled between the 7s and the 6d orbitals, which gives the 14 actinide elements. Because the large number of protons makes their nuclei unstable, all the actinides are radioactive.
Example (PageIndex{2}): Electron Configuration of Mercury
Write the electron configuration of mercury (Z = 80), showing all the inner orbitals.
Given: atomic number
Asked for: complete electron configuration
Strategy:
Using the orbital diagram in Figure (PageIndex{1}) and the periodic table as a guide, fill the orbitals until all 80 electrons have been placed.
Solution:
By placing the electrons in orbitals following the order shown in Figure (PageIndex{2}) and using the periodic table as a guide, we obtain
| 1s2 | row 1 | 2 electrons |
| 2s22p6 | row 2 | 8 electrons |
| 3s23p6 | row 3 | 8 electrons |
| 4s23d104p6 | row 4 | 18 electrons |
| 5s24d105p6 | row 5 | 18 electrons |
| row 1–5 | 54 electrons |
After filling the first five rows, we still have 80 − 54 = 26 more electrons to accommodate. According to Figure (PageIndex{2}), we need to fill the 6s (2 electrons), 4f (14 electrons), and 5d (10 electrons) orbitals. The result is mercury’s electron configuration:
1s22s22p63s23p64s23d104p65s24d105p66s24f145d10 = Hg = [Xe]6s24f145d10
with a filled 5d subshell, a 6s24f145d10 valence shell configuration, and a total of 80 electrons. (You should always check to be sure that the total number of electrons equals the atomic number.)
Exercise (PageIndex{2}): Electron Configuration of Flerovium
Although element 114 is not stable enough to occur in nature, two isotopes of element 114 were created for the first time in a nuclear reactor in 1999 by a team of Russian and American scientists. The element is named after the Flerov Laboratory of Nuclear Reactions of the Joint Institute for Nuclear Research in Dubna, Russia, where the element was discovered in 1998. The name of the laboratory, in turn, honors the Russian physicist Georgy Flyorov. Write the complete electron configuration for element 114.
Answer
s22s22p63s23p64s23d104p65s24d105p66s24f145d106p67s25f146d107p2
The electron configurations of the elements are presented in Figure (PageIndex{2}), which lists the orbitals in the order in which they are filled. In several cases, the ground state electron configurations are different from those predicted by Figure (PageIndex{1}). Some of these anomalies occur as the 3d orbitals are filled. For example, the observed ground state electron configuration of chromium is [Ar]4s13d5 rather than the predicted [Ar]4s23d4. Similarly, the observed electron configuration of copper is [Ar]4s13d10 instead of [Ar]s23d9. The actual electron configuration may be rationalized in terms of an added stability associated with a half-filled (ns1, np3, nd5, nf7) or filled (ns2, np6, nd10, nf14) subshell. Given the small differences between higher energy levels, this added stability is enough to shift an electron from one orbital to another. In heavier elements, other more complex effects can also be important, leading to some of the additional anomalies indicated in Figure (PageIndex{2}). For example, cerium has an electron configuration of [Xe]6s24f15d1, which is impossible to rationalize in simple terms. In most cases, however, these apparent anomalies do not have important chemical consequences.
Additional stability is associated with half-filled or filled subshells.
Summary
Based on the Pauli principle and a knowledge of orbital energies obtained using hydrogen-like orbitals, it is possible to construct the periodic table by filling up the available orbitals beginning with the lowest-energy orbitals (the aufbau principle), which gives rise to a particular arrangement of electrons for each element (its electron configuration). Hund’s rule says that the lowest-energy arrangement of electrons is the one that places them in degenerate orbitals with their spins parallel. For chemical purposes, the most important electrons are those in the outermost principal shell, the valence electrons.
Effective Nuclear Charge ((Z_{eff}))
Figure (PageIndex{1}). Effective nuclear charge in a Li atom. (CC-BY-NC-SA; Kathryn Haas) |
The ideal gas law is easy to remember and apply in solving problems, as long as you get the proper values a
According to Coulomb's law, the attraction of an electron to a nucleus depends only on three factors: the charge of the nucleus (+Z), the charge of the electron (-1), and the distance between the two ((r)). Coulomb's law works well for predicting the energy of an electron in a hydrogen atom (H has only two particles: one nucleus and one electron). It also works for hydrogen-like atoms: any nucleus with exactly one electron (a He+ ion, for example, has one electron). However, Coulomb's law is insufficient for predicting the energies of electrons in multi-electron atoms and ions.
Electrons within a multi-electron atom interact with the nucleus and with all other electrons. Each electron in a multi-electron atom experiences both attraction to the nucleus and repulsion from interactions with other electrons. The presence of multiple electrons decreases the nuclear attraction to some extent. Each electron in a multi-electron atom experiences a different magnitude of (and attraction to) the nuclear charge depending on what specific subshell the electron occupies. The amount of positive charge experienced by any individual electron is the effective nuclear charge ((Z_{eff})). **
For example, in lithium (Li), none of the three electrons 'feel' the full +3 charge from the nucleus (see Cartoon). Rather, each electron 'feels' a (Z_{eff}) that is less than the actual Z and that depends on the electron's orbital. The actual nuclear charge in Li is +3; the 1s electrons experience a (Z_{eff}) =+2.69, and the 2s electron experiences a (Z_{eff}) = 1.28. In general, core electrons (or the electrons closest to the nucleus), 'feel' a (Z_{eff}) that is close to, but less than, the actual nuclear charge (Z). On the other hand, outer valence electrons experience a (Z_{eff}) that is much less than Z.
In summary:
- Core electrons: (Z^* lessapprox Z)
- Valence electrons: (Z^* ll Z)
**You will also see (Z_{eff}) represented as (Z^*): specifically in the section in which you reviewed Periodic Trends, the symbol (Z^*) was used.
Slater's rules for estimating (Z_{eff})
Figure (PageIndex{2}). Diagram illustrating effective nuclear charge according to Slater's rules. |
The (Z_{eff}) can be estimated using a number of different methods; probably the best known and most commonly used method is known as Slater's Rules. Slater developed a set of rules to estimate (Z_{eff}) depending on how many other electrons exist in the atom and on the orbital location of the electron-of-interest. These two factors are important determinants in shielding (see next section), and they are used to calculate a shielding constant ((sigma)) used in Slater's formula:
[Z_{eff}=Z-sigma]
where Z is the actual nuclear charge (the atomic number) and (Z_{eff}) is the effective nuclear charge.
To calculate (sigma), we will write out all the orbitals in an atom, separating them into 'groups'. Each change in shell number is a new group; s and p subshells are in the same group but d and f orbitals are their own group. You write out all the orbitals using parentheses until you get to the group of the electron-of-interest, like this:
(1s)(2s,2p)(3s,3p)(3d)(4s,4p)(4d)(4f)(5s,5p) etc.
**Critical: The orbitals must be written in order of increasing energy!
- Electrons in the same Group(): Each other electron (not counting the electron-of-interest) in the same group () as the chosen electron, contributes 0.35 to (sigma).
Conceptually, this means electrons in the same group shield each other 35%. - Electrons in Groups() to the left:
- If the electron-of-interest is in a d or f subshell, every electron in groups () to the left contributes 1.00 to (sigma).
Conceptually, this means that d and f electrons are shielded 100% by all electrons in the same shell with a smaller value of (l), as well as all electrons in lower shells ((n)). - If the electron-of-interest is in an s or p subshell, all electrons in the next lower shell (n - 1) contribute 0.85 to (sigma). And all the electrons in even lower shells contribute 1.00 to (sigma).
Conceptually, this means that s and p electrons are shielded 85% by the electrons one shell lower, and 100% by all electrons in shells n - 2 or lower.
- If the electron-of-interest is in a d or f subshell, every electron in groups () to the left contributes 1.00 to (sigma).
- 1s electrons: (sigma) of a 1s electron is just (sigma=0.3), no matter the element.
A video explaining how to use Slater's Rules
Example (PageIndex{1}): Fluorine, Neon, and Sodium
What is the (Z_{eff}) experienced by the valence electrons in the three isoelectronic species: fluorine anion (F-), neutral neon atom (Ne), and sodium cation (Na+)?
Solution
Each species has 10 electrons, and the number of core electrons is 2 (10 total electrons - 8 valence), but the effective nuclear charge varies because each has a different atomic number (Z). The approximate (Z_{eff}) can be found with Slater's Rules. For all of these species, we would calculate the same sigma value:
Calculating (sigma): (1s)(2s,2p), (sigma = 2(0.85) + 7(0.35) = 1.7 + 2.45 = 4.15 )
Fluorine anion: (Z_{eff}=9-sigma = 9 - 4.15 = 4.85)

Neon atom: (Z_{eff}=10-sigma = 10 - 4.15 = 5.85)
Sodium Cation: (Z_{eff}=11-sigma = 11 - 4.15 = 6.85)
So, the sodium cation has the greatest effective nuclear charge.
Exercise (PageIndex{1})
Calculate Zeff for a 3d-electron in a zinc (Zn) atom.
Write out the relevant orbitals: (1s)(2s,2p)(3s,3p)(3d) (4s)
Notice that although 4s is fully occupied, we don't include it because in Zn, 4s is higher in energy than 3d, and is thus to the right of the d electrons we are looking at. The electron-of-interest is in 3d, so the other nine electrons in 3d each contribute 0.35 to the value of S. The other 18 electrons each contribute 1 to the value of S.
(S=18(1)+9(0.35)=21.15)
(Z_{eff}=30-21.15=8.85)
So, although the nuclear charge of Zn is 30, the 3d electrons only experience a (Z_eff approx 8.85)!
'Best' values for (Z_{eff})
Slater's rules are a set of simple rules for predicting (sigma) and (Z_{eff}) based on empirical evidence from quantum mechanical calculations. In other words, the (Z_{eff}) calculated from Slater's rules are approximate values. The values considered to be the most accurate are derived from quantum mechanical calculations directly. You can find these values in a nice chart on the Wikipedia article of Effective Nuclear Charge. I've recreated the chart in Figure (PageIndex{3}) for convenience:
(Z_{eff}) modulates attraction
When valence electrons experience less nuclear charge than core electrons, different electrons experiencing different magnitudes of attraction to the nucleus. A modified form of Coulomb's Law is written below, where (e) is the charge of an electron, (Z_{eff}) is the effective nuclear charge experienced by that electron, and (r) is the radius (distance of the electron from the nucleus).
[ F_{eff}=k dfrac{Z_{eff}e^2}{r^2}]
This formula would suggest that if we can estimate (Z_{eff}), then we can predict the attractive force experienced by, and the energy of, an electron in a multi-electron atom, like Li.
The attraction of the nucleus to valence electrons determines the atomic or ionic size, ionization energy, electron affinity, and electronegativity. The stronger the attraction, and the stronger (Z_{eff}), the closer the electrons are pulled toward the nucleus. This in turn results in a smaller size, higher ionization energy, higher electron affinity, and stronger electronegativity.
General Periodic Trends in (Z_{eff})
Close inspection of Figure (PageIndex{3}) and analysis of Slater's rules indicate that there are some predictable trends in (Z_{eff}). The data from Figure (PageIndex{3}) is plotted below in Figure (PageIndex{4}) to provide a visual aid to the discussion below.
Trends in (Z_{eff}) for electrons in a specific shell and subshell
The (Z_{eff}) for electrons in a given shell and subshell generally increases as atomic number increases; this trend holds true going across the periodic table and down the periodic table. Convince yourself that this is true for any subshell by examining Figure (PageIndex{4}).
Inspection of figure (PageIndex{4}) should confirm for you that the (Z_{eff}) increases as Z increases for electrons in any subshell (like the 1s subshell for example, which is plotted above as a red line with square points). You can see this trend as the positive slope in each series. There is one obvious exception in Period 5 in elements 39 (Y) to 41 (Nb; the (Z_{eff}) of 4s actually decreases across these three elements as atomic number increases. There is also an exception between Y and Zr in the 3d subshell, and between Tc and Ru in the 5s subshell.
For valence electrons:
It is useful to understand trends in valence (Z_{eff}) because the valence (Z_{eff}) determines atomic/ionic properties and chemical reactivity. The trends in the valence (Z_{eff}) are not simple because as atomic number increases, the valence shell and/or subshell also changes. The valence (Z_{eff}) is indicated in Figure (PageIndex{4}) as a black line with open circles.
Down the table: As we go down a column of the periodic table, the valence (Z_{eff}) increases. This is a simple trend because type of subshell is consistent and there is an increase only in shell and in atomic number, Z. This trend is best illustrated by inspection of Figure (PageIndex{3}).
Across the table: the trend depends on shell and subshell.
Periods 1-3 (s and p only): As we go across the table in periods 1-3, the shell stays constant as Z increases and subshell changes from s to p. In these periods, there is a gradual increase in valence (Z_{eff}) as we move across any of the first three periods.
Periods 4 and 5 (s, p, and d): Now we have some more complex trends because valence subshell and shell are changing as we increase in atomic number. Notice that the valence (Z_{eff}) generally increases going across a period as long as subshell isn't changing; the exception is within the 4d subshell (elements 39-44 or Y-Ru). In general, going from ((n)s) subshell to ((n-1)d) subshell, there a relatively large increase in valence (Z_{eff}). And in going from ((n-1)d) subshell to ((n)p) subshell, there is a relatively large decrease in (Z_{eff}).
From one period to another: From Figure (PageIndex{4}), we can see that as we increase Z by one proton, going from one period to the next, there is a relatively large decrease in (Z_{eff}) (from Ne to Na, for example). This is because as Z increases by a small interval, the shell number increases, and so the electrons in the valence shell are much farther from the nucleus and are more shielded by all the electrons in the lower shell numbers.

Exercises
Exercise (PageIndex{2})
1. Compare trends in (Z_{eff}) and atomic size. Explain how and why atomic size depends on (Z_{eff}).
2. Compare trends in (Z_{eff}) and ionization energy. Explain how and why ionization energy depends on (Z_{eff}).
1. As (Z_{eff}) increases, the valence electrons are pulled in tighter to the nucleus resulting in a small radius for atoms.
2. As (Z_{eff}) increases, the distance between the valence electrons and the nucleus decreases. This creates a stronger force holding the valence electrons, and thus requires a higher ionization energy to remove a valence electron.
Contributors
Emily V Eames (City College of San Francisco)
Modified or created by Kathryn Haas (khaaslab.com)
